- Upd:5/10/2018
多项式简介
定义
形如$A(x)=\sum_{i=0}^{n-1} a_i x^i$的式子成为多项式
我们把$n$称为该多项式的次数界
需要注意的是,$n-1$次多项式需要用到$n$个数,次数界的定义为最高次项的次数加一
运算法则
设$A(x)$和$B(x)$为多项式,且次数界分别为$n$和$m$,即
$A(x)=\sum_{i=0}^{n-1}a_i x^i$
$B(x)=\sum_{i=0}^{m-1}b_i x^i$
则他们遵循如下的运算法则:
$A(x)+B(x)=\sum_{i=0}^{max(n-1,m-1)} (a_i+b_i)x^i$
$A(x)-B(x)=\sum_{i=0}^{max(n-1,m-1)} (a_i-b_i)x^i$
$A(x)B(x)=\sum_{k=0}^{n+m-2}\sum_{i=0}^{k}a_i b_{k-i} x^k$
其中两个多项式相乘的结果称为它们的卷积,两个次数界为$n$和$m$的多项式相乘的卷积的次数界为$n+m-1$
从上面的定义中,我们可以看到求多项式的卷积复杂度为$O(n^2)$
使用快速傅里叶变换,可将多项式乘法的复杂度降至$O(n\log n)$
复数简介
复数的代数形式
形如$a+bi$的数我们称为复数,其中$i$为$\sqrt{-1}$
对应的,我们可以用二维平面上的点$(a,b)$来表示这个复数
复数的运算法则和实数类似,你只需要把复数看成一个式子就行了
复数的三角形式
上面提到的$a+bi$称为复数的代数形式
除此之外,复数还可以用三角函数的形式来表示
如下图所示:
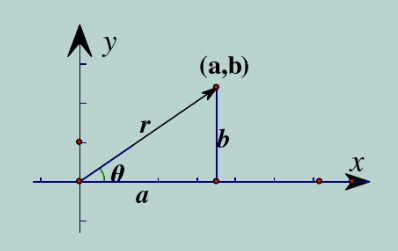
我们知道复数$a+bi$对应着复平面上的点$(a,b)$,也对应着复平面上的一个向量
这个向量的长度叫作复数$a+bi$的模,记作|$a+bi$|,一般情况下用字母$r$表示
这个向量与$x$轴正方向有一个夹角,称为辐角,一般情况下用希腊字母$\theta$表示
那么显然$a=r\cos\theta$,$b=r\sin\theta$
带入到代数形式的表达式中,可以得到它的三角形式:$a+bi=r(\cos\theta+i\sin\theta)$
定理:两复数相乘,模长相乘,辐角相加
证明:设$z_1=r_1(\cos x+i\sin x)$,$z_2=r_2(\cos y+i\sin y)$
则$z_1 z_2=r_1 r_2 [\cos x\cos y-\sin x\sin y+i(\cos x\sin y+\cos y\sin x)]$
$=r_1 r_2[\cos(x+y)+i\sin(x+y)]$
复数的指数形式
欧拉公式:$e^{i\theta}=\cos\theta+i\sin\theta$
证明:将$e^x,\sin x,\cos x$按照泰勒公式进行展开得到它们的泰勒级数:
$e^x=1+\frac{x}{1!}+\frac{x^2}{2!}+\frac{x^3}{3!}+…$
$\cos x=1-\frac{x^2}{2!}+\frac{x^4}{4!}-\frac{x^6}{6!}+…$
$\sin x=x-\frac{x^3}{3!}+\frac{x^5}{5!}-\frac{x^7}{7!}$
将$x=i\theta$带入得:
$e^{i\theta}=1+\theta i-\frac{\theta^2}{2!}-\frac{\theta^3}{3!}i+\frac{\theta^4}{4!}+\frac{\theta^5}{5!}i-\frac{\theta^6}{6!}-\frac{\theta^7}{7!}i+…$
$e^{i\theta}=(1-\frac{\theta^2}{2!}+\frac{\theta^4}{4!}-\frac{\theta^6}{6!}+…)+i(\theta-\frac{\theta^3}{3!}+\frac{\theta^5}{5!}-\frac{\theta^7}{7!}+…)$
即$e^{i\theta}=\cos\theta+i\sin\theta$
证毕
将欧拉公式带入到三角形式的表达式中就能得到复数的指数形式表达式:$z=r(\cos\theta+i\sin\theta)=re^{i\theta}$
单位复数根
在复数域内,有且仅有n个数,使得这个数的n次方等于1,我们把这样的数称为单位复数根,记作 $\omega_{n}^{i} (i\epsilon [0,n-1])$
将$\theta=2\pi$带入到欧拉公式中得到:$e^{2\pi i}=1$
所以$\omega_{n}^{k}=(e^{\frac{2\pi i}{n}})^k$
消去引理:$\omega_{dn}^{dk}=\omega_{n}^{k}$
证明:$\omega_{dn}^{dk}=(e^{\frac{2\pi i}{dn}})^{dk}=(e^{\frac{2\pi i}{n}})^k=\omega_{n}^{k}$
折半引理:$(\omega_{n}^{k})^2=\omega_{n/2}^{k}$
证明:将$d=\frac{1}{2}$带入消去引理即可得证
求和引理:$\sum_{i=0}^{n-1} (\omega_{n}^{k})^i=0$ ($k$不是$n$倍数)
证明:利用等差数列求和公式:原式$=\frac{(\omega_{n}^{k})^n-1}{\omega_{n}^{k}-1}=\frac{0}{\omega_{n}^{k}-1}$
因为分母不能为$0$,所以${\omega_{n}^{k}}$不能为$1$,所以$k$不是$n$倍数
循环性质:$(\omega_{n}^{k})^p=\omega_{n}^{pk}=\omega_{n}^{(pk\mod{n})}$
证明:$\omega_{n}^{kp}=\omega_{n}^{(kp\mod n+\left \lfloor \frac{kp}{n} \right \rfloor n)}=\omega_{n}^{(kp \mod n)}$
对称性质:$w_{n}^{k+\frac{n}{2}}=-w_{n}^{k}$
证明:$w_{n}^{k+\frac{n}{2}}=e^{\frac{2\pi ki}{n}+\pi i}=w_{n}^{k} e^{\pi i}=-w_{n}^{k}$
离散傅里叶变换
多项式的两种表示方法
像开头提到的多项式,都是以系数形式表示的
也就是将$n$次多项式$A(x)$的系数$a_0,a_1,…,a_{n-1}$看成$n$维向量$\vec{a}=(a_0,a_1,…,a_{n-1})$,$\vec{a}$就是$A(x)$的系数表示
事实上除了上面的$A(x)=\sum_{i=0}^{n-1}a_i x^i$的系数表示方法,多项式还有一种表示方法:点值表示法
一个多项式$A(x)$的点值表达就是一个由$n$个点值对多组成的集合:{$(x_0,y_0),(x_1,y_1),…,(x_{n-1},y_{n-1})$},对于$0<=k<=n-1$,所有$x_k$各不相同,记作:$y_k=A(x_k)$
而离散傅里叶变换就是要快速求出多项式在这$n$的点的值
Cooley-Tukey算法
Cooley-Tukey算法是一种基于分治的算法
我们取$n$个$n$次单位根$w_{n}^{0},w_{n}^{1},…,w_{n}^{n-1}$进行求值:$A(w_{n}^{k})=\sum_{i=0}^{n-1}a_i w_{n}^{ki}$
点值向量$\vec{y}=(A(w_{n}^{0}),…,A(w_{n}^{n-1}))$称为$\vec{a}=(a_0,…,a_n)$的离散傅里叶变换
接下来我们按照奇偶分开来算:
$A(w_{n}^{k})=\sum_{i=0}^{n-1}a_i w_{n}^{ki}$
$=\sum_{i=0}^{\frac{n}{2}-1}a_{2i}w_{n}^{2ki}+w_{n}^{k}\sum_{i=0}^{\frac{n}{2}-1}a_{2i+1}w_{n}^{2ki}$
$=\sum_{i=0}^{\frac{n}{2}-1}a_{2i}w_{\frac{n}{2}}^{ki}+w_{n}^{k}\sum_{i=0}^{\frac{n}{2}-1}a_{2i+1}w_{\frac{n}{2}}^{ki}$(折半引理)
而$A(w_{n}^{k+\frac{n}{2}})=\sum_{i=0}^{\frac{n}{2}-1}a_{2i}w_{\frac{n}{2}}^{ki}-w_{n}^{k}\sum_{i=0}^{\frac{n}{2}-1}a_{2i+1}w_{\frac{n}{2}}^{ki}$(对称性质)
这样我们的子问题就变成了求$\frac{n}{2}$个单位根的点值,规模缩小了一半,时间复杂度$O(n\log n)$
这样的操作算法导论中称为蝶形变换
中文伪代码如下:

快速傅里叶逆变换
求值与插值
对于一个多项式,如果知道它的系数表达式,我们很容易求出它的点值表达式,这一过程成为求值
如果知道它的点值表达式,让你求它的系数表达式,这一过程称为插值
定理:当插值多项式的次数界等于已知点值对的数目时,插值才是明确的
证明:$y_k=A(x_k)$等价于下式:
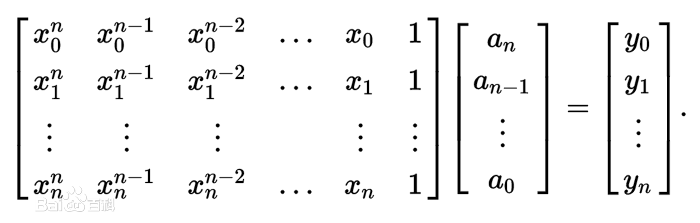
其中,左边的矩阵称为范德蒙矩阵,其行列式$Det=\prod_{0\leq j<k\leq n-1}(x_k-x_j)$
如果所有的$x_k$均不同,那么$Det\neq 0$,范德蒙矩阵可逆
因此给定点值表达,能够唯一确定系数表达
所以如果我们知道了一个多项式的点值表示,就可以通过矩阵求逆的方法来算出系数向量
现在我们得到了点值表达式,那么如何求系数表达式呢?
矩阵求逆的复杂度是$O(n^3)$的,范德蒙矩阵求逆可以优化至$O(n^2)$,但是复杂度依旧很高
我们考虑构造一个现成的能算的东西进行优化
构造逆矩阵
我们现在已经得到了这样的方程:
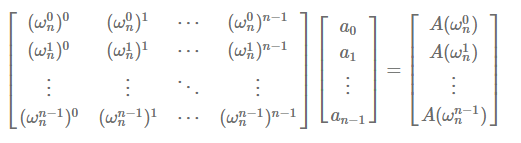
记系数矩阵为$V$,构造下面的矩阵:$d_{ij}=w_{n}^{-ij}$
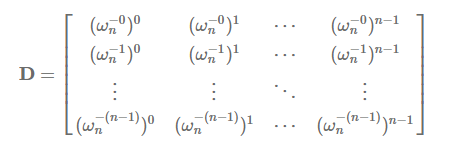
它们相乘的结果$E=DV$满足$e_{ij}=\sum_{k=0}^{n-1}w_{n}^{k(j-i)}$
当$i=j时$,$e_{ij}=n$
当$i\neq j时$,$e_{ij}=\sum_{k=0}^{n-1}(w_{n}^{(j-i)})^k=0$(求和引理)
所以$\frac{1}{n}D$就是我们需要的逆矩阵,如下图:
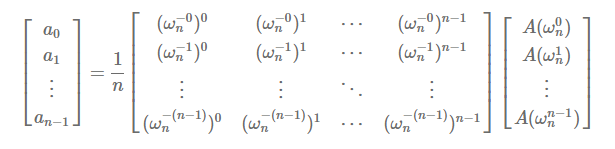
这就相当于我们把单位复数根$w_{n}^{k}$换成$w_{n}^{-k}$再做一遍离散傅里叶变换结果除以$n$就行了
模板代码
- 【UOJ#34】多项式乘法AC传送门
|
|