• 本文为博主原创，未经许可不得转载

从有限状态自动机说起

定义

有限状态自动机，简称自动机，具有识别字符串的功能

若一个自动机$A$能识别字符串$S$，则记$A(S)=true$，否则$A(S)=false$

组成

$alpha$：字符集，一般为$26$个字母组成的集合

$state$：状态集合，即自动机上的点，其本质为若干字符串组成的集合

$init$：初始状态，一般为空集

$end$：结束状态集合，又称可接受态，表示读入新字符后可进行转移的状态

$trans$：状态转移函数，$trans(G,ch)$表示从状态$G$读入字符$ch$后所到达的状态

根据这些定义，我们知道自动机$A$能识别的字符串$S$必定满足$trans(init,S)\subset end$

后缀自动机的构造原理

朴素状态后缀自动机

给定字符串$S$,$S$的后缀自动机($SAM$，以下简称$SAM$)是一个能识别$S$的所有后缀的自动机

即$SAM(x)=true$，当且仅当$x$是$S$的后缀

考虑字符串aabbabd，我们可以讲该字符串的所有后缀插入一个$Trie$树中，就像下图那样。

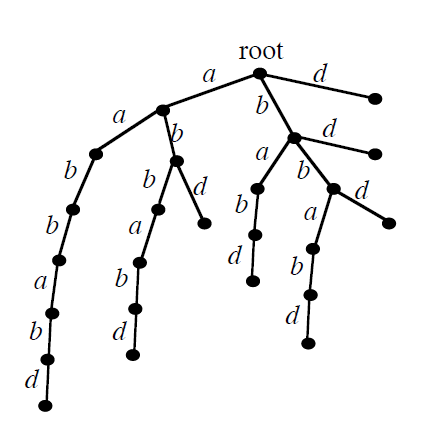
那么初始状态就是根，状态转移函数就是这颗树的边，结束状态集合就是所有的叶子

这样我们就得到了一个$S$的朴素状态后缀自动机

我们发现它的节点数和边数都是$O(n^2)$的，时间和空间上都无法承受

考虑进行优化

最简状态后缀自动机

在上面的朴素状态自动机里，每个结点表示一个子串，我们发现一些结点可以识别的字符串的集合是相同的，这就是我们进行优化的根源

对于可以识别相同的字符串的状态，我们称之为等价的状态，我们可以把它们压缩为一个状态，这样就可以大大节省结点数量

注：一个状态$G$能识别字符串$x$，当且仅当$Gx$是$S$的后缀

那么我们如何判断两个状态是等价的呢？

这里引入一个$Right$集合的概念

设子串$x$在母串$S$中的 [$l_1,r_1$) , [$l_2,r_2$) , [$l_3,r_3$) , [$l_n,r_n$) 位置出现 (注意：区间是左闭右开的)

那么$Right(x)=${$r_1,r_2,r_3,……,r_n$}

如$S=AB{\color{Red}B}{\color{Red} B}{\color{Red} A}{\color{Red} B}{\color{Red}B }{\color{Red}A }BBB{\color{Red}B }{\color{Red} B}{\color{Red}A }$,$x=BBA$

则$Right(x)=${$6,9,15$}

同时我们发现：

状态 $AB{\color{Red}B}{\color{Red} B}{\color{Red} A}$ 可以识别串${\color{Red} B}{\color{Red}B }{\color{Red}A }BBB{\color{Red}B }{\color{Red} B}{\color{Red}A }$

状态 $AB{\color{Red}B}{\color{Red} B}{\color{Red} A}{\color{Red} B}{\color{Red}B }{\color{Red}A }$ 可以识别串$BBB{\color{Red}B }{\color{Red} B}{\color{Red}A }$

状态 $AB{\color{Red}B}{\color{Red} B}{\color{Red} A}{\color{Red} B}{\color{Red}B }{\color{Red}A }BBB{\color{Red}B }{\color{Red} B}{\color{Red}A }$ 只能识别空串

即一个状态可以识别的字符串的集合只有该状态的$Right$集合决定

对于两个子串$a,b,$如果$Right(a)=Right(b)$，那么$trans(init,a)=trans(init,b)$

所以我们可以把$Right$集合相同的状态压缩成一个状态

我们把压缩后的自动机称为最简状态后缀自动机，可以证明它的状态数是线性的

假如现在我们已经得到了这个最简状态后缀自动机，以及每个结点的$Right$集合，那么只需要再给定一个长度$len$就可以确定子串了

考虑对于一个$Right$集合，如果长度l，r合适，那么区间[l,r]内的长度也一定合适

比如上面的例子中,$A$和$BBA$是合适的，所以可以令$l=1,r=3,$则当长度$len=2$时，$BA$也是合适的

对于一个状态$G$，我们令$Min(G)=l,Max(G)=r$，则$G$的子串的合适长度的范围就是$[Min(G),Max(G)]$

如在上面的例子中，$Min(x)=1,Max(x)=3$

$Max(x)$表示的意义是：这个串如果更长的话，$right(x)$ 中的某些位置就无法和串匹配了

$Min(x)$表示的意义是：这个串如果更短的话，某些不属于 $right(p) $的位置也能和串匹配了

线性复杂度的证明

• 温馨提示：证明过程纯属理性的愉悦，读者可以自行选择跳过

先证明状态数是线性的：

考虑两个状态$a,b,$若$Right(a)$和$Right(b)$有交集

因为一个子串至多属于一个状态，所以状态$a，b$中不会有相同的子串

所以$[Min(a),Max(a)]$和$[Min(b),Max(b)]$没有交集

不妨设$Max(a)<Min(b)，$那么状态$a$中所有串都比$b$中的短，所以$a$中的串都是$b$中串的后缀

因此，$a$中某串的出现位置，$b$中某串也必然出现了

所以$Right(a)$是$Right(b)$的真子集

所以就有如下结论：任意两个状态的$Right$集合要么不想交，要么一个是另一个的真子集

事实上，所有状态的$Right$集合构成了一个树形结构，如下图

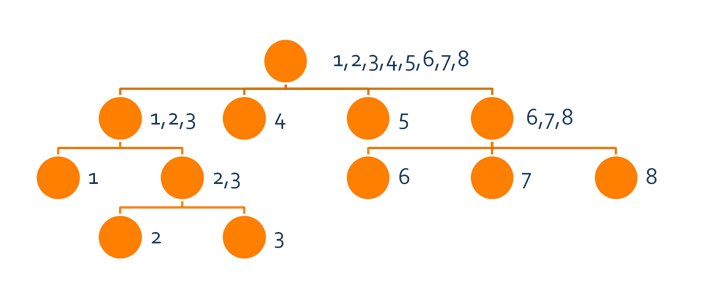
我们把这棵树称为$parent$树

在这颗树中，叶子结点有$n$个，内部结点至少有$2$个儿子，所以结点个数最多为$2n$个

这就是$SAM$为什么要开$2$倍数组的原因 (切记，切记，山神因为这个省选$gg$了)

这样我们就证明了$SAM$的状态数是线性的

下面我们来证明边数也是线性的：

我们首先来求一棵$SAM$的生成树，因为点数是$2n$，那么树上的边数就是$2n-1$

对于一条非树边$a\rightarrow b$，SAM上的一个后缀的路径可以表示为$(init\rightarrow a)+(a\rightarrow b)+(b\rightarrow end)$

所以一个后缀对应一条非树边，一条非树边可以对应到若干个后缀

所以非树边最多只有$n$条

所以边数也是线性的

性质与结论

（1）设两个状态$G、H，$若$Right(G)$是$Right(H)$的真子集，且$Right(H)$在是满足该条件的$Right(H_i)$中是最小的，那么我们称$H$为$G$的$parent$

注：集合$A$的大小是指集合中元素的多少，用$|A|$表示

（2）$Max(parent(G))=Min(G)-1$

证明：

考虑一个状态$G，G$的范围是$[Min(G),Max(G)]，$设$H$为$parent(G),$因为$|Right(H)|>|Right(G)|$

所以对于$Min(G)-1，$它的出现位置的右端点必定是超出了$Right(G)，$而属于$Right(H)$的范围，所以有如下结论：

（3）母串$S$的每个子串必然在SAM的某个状态里

（4）一个状态的$Right$集合等于该状态在$parent$树中所有儿子$Right$集合的并集

（5）两个状态的$Right$集合要么不相交，要么一个是另一个的真子集

状态的转移

考虑一个状态$G$，它的$Right$集为{$r_1,r_2,r_3,……,r_n$}，假如有一条$G\rightarrow H $且标号为$c$的边，考虑$H$的$Right$集

由于多了一个字符，$G$的$Right$集中只有$S[r_i]=c$的符合要求，那么$H$的$Right$集为{$r_i|S[r_i]==c$}

所以有如下两条结论：

（1）显然$|Right(G)|>|Right(H)|$，且$Right(H)$是$Right(G)$的真子集，所以$Max(H)>Max(G)$

（2）如果从$G$出发有标号为$c$的边，那么从$parent(G)$出发必然也有

构造过程

$SAM$的构建是$online$的，每插入一个字符完成一次状态转移，所以我们只需要考虑假设已经建好了前$i$个字符的$SAM$，然后插入了$S[i+1]$的情况

设当前字符串为$T$，新插入的字符为$x，T$的长度为$len$

则新加入一个$x$，就多了$len$个子串，且这些子串都是$Tx$的后缀

我们考虑所有表示T的后缀的结点（可接受态结点）$v_1,v_2,……v_n，$它们的$Right$集中包含$len$

由于必然存在一个状态$p=trans(init,T)$使得它的$Right$集中仅有$len$这个元素，那么其它的结点$v_1,v_2…….$在$parent$树中是$p$的祖先

可以用$parent$指针得到它们，不妨把这些结点按照从后代到祖先的顺序排序

我们新添加一个字符$x$后，令$np=trans(init,Tx),$则$Right(np)=len+1$

对于出发没有标号为$x$的边的结点$v$，它的$Right$集中只有$r_n$是符合要求的，直接连一条$v\rightarrow np$的边即可

对于第一个出发有标号为$x$的边的结点$v_p$，设它的$Right$集为{$r_1,r_2,……r_n$}，令$trans(v_p,x)=q$，则$q$的$Right$集为{$r_i+1|S[r_i]==x$}

因为$v_p\rightarrow q$有标号为$x$的边，所以$q$是一个可接受态结点，所以要在$q$的$Right$集中插入$len+1$

但是直接插入有可能会使$Max(q)$变小从而引发一系列问题

如果$Max(q)=Max(p)+1$自然不会有问题，直接令$parent(np)=q$即可

注：因为$np$的$Right$集为{$L+1$},它必定是$q$的$Right$集的真子集，所以$Parent(np)=q$

否则我们把$q$分成两个结点$q$和$nq$，$q$负责维护原来的状态转移，$nq$负责维护插入字符$x$之后的状态转移

显然$Right(nq)=Right(q)\cup L+1$ , $Max(nq)=Max(np)+1$

由于$Right(q)$和$Right(np)$是$Right(nq)$的真子集，所以$parent(q)=parent(np)=nq$

我们注意到$L+1$对$trans(init,q)$的转移是没有影响的，所以可以直接把$q$的信息赋值给$nq$

然后对于$trans(v,x)=q$的结点$v$，由于已经插入了$x$，把$trans(v,x)$设为$nq$即可

整个过程如下图所示：

在很多时候，我们需要用到Right集的大小，如何求Right集的大小呢？

我们发现构建好的SAM是个有向无环图，我们对它进行拓扑排序，parent树上叶子节点|Right|设为1，然后按照拓扑序更新parent即可

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

int cnt=1,last=1;
void extend(int x){
	int np=++cnt,p=last; Right[np]=1;
	mx[np]=mx[p]+1;  last=np;
	while(p&&!tr[p][x])  tr[p][x]=np,p=par[p];
	if(!p)  par[np]=1;
	else{
		int q=tr[p][x];
		if(mx[q]==mx[p]+1)  par[np]=q;
		else{
			int nq=++cnt; mx[nq]=mx[p]+1;
			memcpy(tr[nq],tr[q],sizeof(tr[q]));
			par[nq]=par[q];  par[q]=par[np]=nq;
			while(p&&tr[p][x]==q)  tr[p][x]=nq,p=par[p];
		}
	}
}
void topsort(){
	for(int i=1;i<=cnt;++i)  c[mx[i]]++;
	for(int i=1;i<=n;++i)    c[i]+=c[i-1];
	for(int i=1;i<=cnt;++i)  id[c[mx[i]]--]=i;
	for(int i=cnt;i;--i)  Right[par[id[i]]]+=Right[id[i]];
}